For this lab, we will be using the igraph package. Install the package before beginning the lab:
install.packages("igraph")
If the package does not download due to the UWS proxy server, see Lab 5 for further information on installing packages.
Once installed. Load the library:
library("igraph")
To create a graph, we can use the formula interface or provide an adjacency matrix.
To create a graph from an adjacency matrix, we must first create the matrix. An adjacency matrix \(A\) contains \(N\) rows and columns, where \(N\) is the number of vertices. The element \(a_{i,j}\) of \(A\) is the element from the \(i\)th row and the \(j\)th column. If there is an edge between the \(i\)th vertex and \(j\)th vertex, then \(a_{i,j} = 1\). If there is no edge, then \(a_{i,j} = 0\).
We can first make a \(4\times 4\) matrix, containing all zeros:
A = matrix(0, 4, 4)
Then add the edges by allocating ones. We will make the same graph shown above in g1. We want to connect the first vertex to the second, third and fourth vertices:
A[1, c(2, 3, 4)] = 1
We also want to connect the second vertex to the first and fourth:
A[2, c(1, 4)] = 1
We connect the thrid vertex to the first:
A[3, 1] = 1
And connect the fourth vertex to the first and second:
A[4, c(1, 2)] = 1
Giving us:
print(A)
## [,1] [,2] [,3] [,4]
## [1,] 0 1 1 1
## [2,] 1 0 0 1
## [3,] 1 0 0 0
## [4,] 1 1 0 0
Notice that the matrix is symmetric. Adjacency matrices for undirected graphs are always symmetric, showing that the edges can be followed from either direction.
We create the matrix with:
g2 = graph.adjacency(A)
and visualise it:
plot(g2)
Notice that the edges in the plot of g2 have arrows, implying that it is a directed graph. Examine the help page of the function graph.adjacency and work out how to make the graph undirected.
We can also create a graph using an edge list. An edge list is an \(M\times 2\) matrix, containing \(M\) edges. Each row of the edge list provide the start and end vertices. For example:
el = matrix(c("A", "A", "A", "B", "B", "C", "D", "D"), 4, 2)
print(el)
## [,1] [,2]
## [1,] "A" "B"
## [2,] "A" "C"
## [3,] "A" "D"
## [4,] "B" "D"
We then create the graph:
g4 = graph.edgelist(el, directed = FALSE)
plot(g4)
We saw in the lecture that we are able to create an Erdős-Renyi Graph once given the parameters \(n\) (the number of vertices) and \(p\) (the probability of an edge appearing).
To create and Erdős-Renyi Graph:
g.er = erdos.renyi.game(n = 100, p = 0.1)
plot(g.er, vertex.size = 5)
In the plot command, we reduced the vertex size so we can see the edges more clearly. Run the plot command without vertex.size = 5 to see the difference.
To create a Barabási–Albert Graph, we must provide \(n\) (the number of vertices). We can also provide the \(k\) (the power) and \(m\) (the number of edges to add to each new vertex).
g.ba = barabasi.game(n = 100, directed = FALSE)
plot(g.ba, vertex.size = 5)
In this section, we will examine some of the functions that that available for us to examine properties of graphs.
By visually examining the two graphs above, which looks denser? Use the function graph.density to compute the density of each graph and compare the results to your guess.
The diameter is the longest shortest path. Which of the two graphs do you expect to have the largest diameter? Use the function diameter to compute the diameter of each graph.
What do you expect the degree distribution of each graph to look like? We can compute the degree of each vertex using the function degree. We can also compute the degree distribution of the graph using the function degree.distribution. Use the help pages to understand the output.
Which vertex is most central according to Degree Centrality?
We defined the closeness centrality of a vertex \(v\) as the sum of the distance from \(v\) to all other vertices. To compute the closeness of each vertex, we use:
closeness(g.ba)
## [1] 0.003788 0.002762 0.003333 0.003311 0.002762 0.002793 0.002513
## [8] 0.002762 0.002890 0.002347 0.002513 0.002941 0.002513 0.002577
## [15] 0.002058 0.002326 0.002513 0.002778 0.002551 0.002193 0.001946
## [22] 0.002762 0.002315 0.002500 0.002538 0.002033 0.002762 0.002513
## [29] 0.002513 0.001894 0.002513 0.001908 0.002809 0.001887 0.002283
## [36] 0.002041 0.002058 0.001938 0.002283 0.002066 0.001916 0.001923
## [43] 0.001618 0.002041 0.001639 0.002500 0.001416 0.001887 0.002203
## [50] 0.002283 0.002513 0.002513 0.002203 0.002513 0.001887 0.002513
## [57] 0.002033 0.001634 0.001634 0.002203 0.002525 0.002024 0.002183
## [64] 0.002500 0.002203 0.001618 0.002513 0.002193 0.002778 0.001623
## [71] 0.002041 0.001634 0.002294 0.002762 0.001894 0.002283 0.002513
## [78] 0.002058 0.002513 0.002525 0.002500 0.001613 0.001634 0.001908
## [85] 0.001812 0.002283 0.001629 0.001873 0.002762 0.001401 0.002500
## [92] 0.001634 0.001244 0.002183 0.002024 0.002024 0.001718 0.002193
## [99] 0.002513 0.002513
This does not look right. The sum of differences should be an integer, but the R output is a set of real values.
Read the R help page for closeness to find what R is computing. Then work out which of the vertices is the most central with respect to closeness centrality.
Betweenness centrality measures how often a vertex is used in shortest paths. We can compute betweenness using:
betweenness(g.er)
## [1] 171.33 28.29 48.91 74.90 48.95 57.37 41.30 36.59 63.63 20.07
## [11] 44.09 40.90 63.85 23.21 81.56 26.37 39.32 122.25 42.47 12.23
## [21] 23.68 27.77 21.35 55.03 47.72 173.35 36.42 27.46 84.79 114.21
## [31] 71.06 70.04 116.84 32.07 43.49 58.11 58.96 12.69 109.86 12.58
## [41] 40.13 55.89 61.97 18.53 66.74 25.08 19.68 81.12 61.62 42.52
## [51] 159.20 163.17 12.82 87.75 54.75 13.84 54.30 23.70 51.59 40.95
## [61] 59.32 65.92 106.04 92.58 107.34 95.37 121.86 16.12 124.45 113.40
## [71] 56.43 89.08 16.42 35.52 34.97 38.95 56.50 125.17 77.38 50.25
## [81] 86.64 77.95 39.86 61.29 36.61 28.60 66.14 34.50 61.11 47.45
## [91] 56.96 36.04 10.90 116.02 69.48 55.12 118.41 83.14 83.59 161.71
Is the centre the same for all three centrality measures? Examine this for the Erdős-Renyi graph and Barabási–Albert graph.
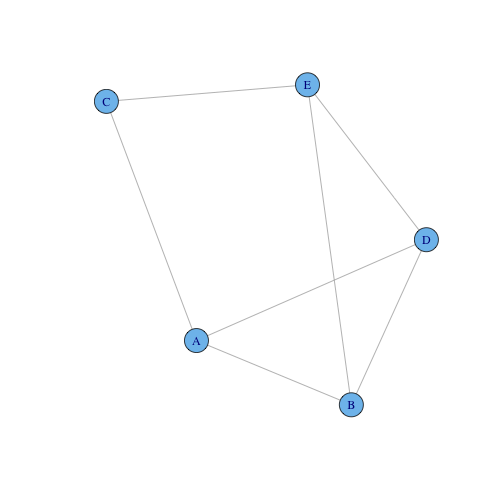
Using the following graph:
g3 = graph.formula(A - B, A - C, A - D, B - D, B - E, E - D, C - E)
plot(g3)
Calculate the:
- Degree Distribution
- Degree Centrality
- Closeness Centrality
- Betweenness Centrality
using the methods shown in the lecture. Then check your answer using the R functions.